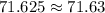Question

The diagram above shows a rectangle inscribed in a circle AB=10 and AC =12 caculate the total surface area of the shaded part

​

Answer 1

`71.63 \: \: \mathrm{cm^2 }`

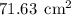
Explanation:

Once we know the diameter of the circle, we can figure out the problem.

The diameter of the circle = The diagonal of the rectangle inscribed in the circle

To find the diagonal of the rectangle, we can use a formula.

`d=√(w^2 + l^2)`

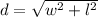
The width is 10 cm and the length is 12 cm.

`d=√(10^2 + 12^2)`

`d \approx 15.62`

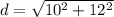
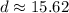
The diagonal of the rectangle inscribed in the circle is 15.62 cm.

The diameter of the circle is 15.62 cm.

Find the area of the whole circle.

`A=\pi r^2`

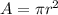
The
`r` is the radius of the circle, to find radius from diameter we can divide the value by 2.

`r = (d)/(2)`

`r=(15.62)/(2)`

`r=7.81`

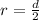
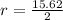
Let’s find the area now.

`A=\pi (7.81)^2`

`A \approx 191.625`

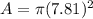
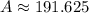
Find the area of rectangle.

`A=lw`

Length × Width.

`A = 12 * 10`

`A=120`

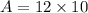
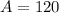
Subtract the area of the whole circle with the area of rectangle to find area of shaded part.

`191.625-120`

`71.625 \approx 71.63`