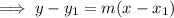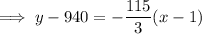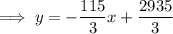Answer:
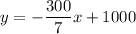
Explanation:
Method 1 (see attachment 1 with red line)
Plots the points on a graph and draw a line of best fit, remembering to ensure the same number of points are above and below the line.
Use the two end-points of the line of best fit to find the slope:

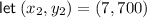
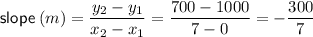
Input the found slope and point (0, 1000) into point-slope form of a linear equation to determine the equation of the line of best fit:
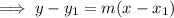
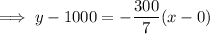
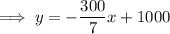
Method 2 (see attachment 2 with blue line)
If you aren't able to plot the points, you should be able to see that the general trend is that as x increases, y decreases. Therefore, take the first and last points in the table and use these to find the slope:
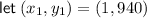
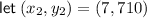
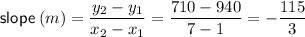
Input the found slope and point (1, 940) into point-slope form of a linear equation to determine the equation of the line of best fit: