Question

Show that 3-underroot2 is irrational​

Answer 1

Explanation:

Hello,

Basically, we need to prove that
`√(2)` is irrational

Let s assume that
`√(2)` is rational

it means that we can find p and q (q different from 0) two integers with no common factors other than 1

so that

`√(2)=(p)/(q)`

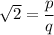
And then we can write that

`2=(p^2)/(q^2)\\<=> p^2=2q^2`

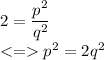
So
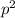`p^2` is even so it means that p is even

so
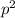`p^2` is divisible by 2*2=4

as
`p^2=2q^2` it means that
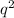`q^2` is even, meaning q is even

wait, p and q are then even !? but by definition they have no common factors. This is not possible.

so our assumption that
`√(2)` is rational is false

So it means that this is irrational

and then
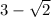`3-√(2)` is irrational too

Hope this helps