Question

Please show step by step of working out the value of r for which is A minimum and calculate the minimum surface area of the container.

The total surface area, Acm^2, of each container is modelled by function A= πr^2+100/r.

(remember to use the derivative to show you have found the minimum)​

Answer 1

A = 59.63cm^2

Explanation:

You have the following function for the surface area of the container:

`A=\pi r^2+(100)/(r)` (1)

where r is the radius of the cross sectional area of the container.

In order to find the minimum surface are you first calculate the derivative of A respect to r, to find the value of r that makes the surface area a minimum.

`(dA)/(dr)=(d)/(dr)[\pi r^2+(100)/(r)]\\\\(dA)/(dr)=2\pi r-(100)/(r^2)` (2)

Next, you equal the expression (2) to zero and solve for r:

`2\pi r-(100)/(r^2)=0\\\\2\pi r=(100)/(r^2)\\\\r^3=(50)/(\pi)\\\\r=((50)/(\pi))^(1/3)`

Finally, you replace the previous result in the equation (1):

`A=\pi ((50)/(\pi))^(2/3)+(100)/(((50)/(\pi))^(1/3))}`

`A=59.63`

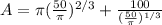
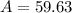
The minimum total surface area is 59.63cm^2