Question

Solve the equation by factoring:

x² – 5x = 14
a. x= -2 or 7
b. x= 2 and -7
C. X= -2 or -7
d. x = 2 or 7

Answer 1

a. -2 or 7

Explanation:

`x^2-5x=14\\\\x^2-5x-14=0\\\\x^2+2x-7x-14=0\\\\x(x+2)-7(x+2)=0\\\\(x+2)(x-7)=0\\\\x+2=0\quad\vee\quad x-7=0\\\\x=-2\quad\vee\quad x=7`

Answer 2

The two possible solutions are x = 7, or x = -2

which agree with answer a) in the list of options

Explanation:

Start by moving all terms to one side of the equal sign, and then factoring out the constant term:

`x^2-5x-14=0`

The constant term "-14" has ossible factors: (-1), (1) (-2), (2), (-7), (7), (-14), (14) and we look for a pair whose combining results in "-5" (the coefficient of the middle term. We find (-7) and (2) the appropriate factors, so we use then to split the middle term and then factor by grouping:

`x^2-5x-14=0\\x^2-7\,x+2\,x-14=0\\x(x-7)+2(x-7)=0\\(x-7)\,(x+2) = 0`

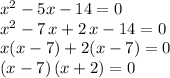
Then if the product of these two binomial factors is zero, it means that the first binomial is zero, or the second one is zero. That is:

( x - 7 ) = 0 which means x = 7

or

( x + 2 ) = 0 which means x = -2

So the two possible solutions are x = 7, or x = -2