Question

HELP ASAP PLEASE
I JUST NEED WORK SHOWN BUT ASAP

Answer 1

s = 25.33m

θ = 60.65°

12.37m

A = 160m^2

Explanation:

The pyramid has a side base of 35m and a height of 22m.

side base = b = 35m

height of the pyramid = h = 22m

To calculate the slant edge of the pyramid, you first calculate the diagonal of the squared base of the pyramid.

You use the Pythagoras theorem:

`d=\sqrt{((35)/(2))^2+((35)/(2))^2}=24.74`

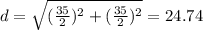
With the half of the diagonal and the height, and by using again the Pythagoras theorem you can calculate the slat edge:

`s=\sqrt{((24.74)/(2))^2+(22)^2}=25.23`

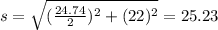
The slant edge of the pyramid is 25.33m

The angle of the base is given by:

`\theta=sin^(-1)((h)/(s))=sin^(-1)((22)/(25.23))=60.65\°`

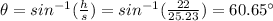
The angle of the base is 60.65°

The distance between the corner of the pyramid and its center of its base is half of the diagonal, which is 24.74/2 = 12.37m

The area of one side of the pyramid is given by the following formula:

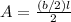`A=((b/2)l)/(2)` (1)

l: height of the side of pyramid

then, you first calculate l by using the information about the side base and the slant.

`l=\sqrt{s^2-((b)/(2)^2)}=\sqrt{(25.33)^2-((35)/(2))^2}\\\\l=18.31m`

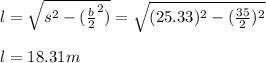
Next, you replace the values of l and b in the equation (1):

`A=((35/2)(18.31))/(2)=160m^2`

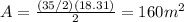
The area of one aside of the pyramid is 160m^2