Question

The mean and variance are known as the _____
of a distribution.

Answer 1

The mean and variance are known as the parameters of a distribution.

Explanation:

The mean and the variance are parameters of a distribution. Parameters are constantly estimated in Statistics using samples of values of a population because they are often unknown.

They characterize a quantitative aspect of a probability distribution, and completely determined the distribution. For example, in the normal distribution, the mean,
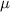`\\ \mu`, and the variance,
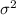`\\ \sigma^(2)`, determined this distribution.

Most of the time, the standard deviation,
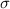`\\ \sigma`, is more used than the variance because is in the same units that the mean.

In this way, we can say that these parameters "tell us" where the central point of the distribution is (this is the case for the mean), and also, how spread the values of a probability distribution are (the case for variance or the standard deviation).