Answer:

Option A is the correct option.
Explanation:
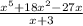
Factor out X from the expression
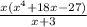
Add and subtract
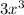
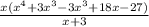
Write 18x as a difference
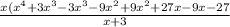
factor out
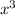 from the expression
from the expression
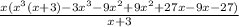
Factor out
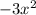 from the expression
from the expression
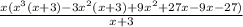
factor out 9x from the expression
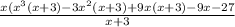
Factor out -9 from the expression
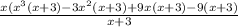
factor out x+3 from the expression
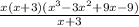
Reduce the fraction with X+3
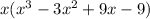
Distribute X through the parentheses

hope this helps...
Good luck on your assignment...