Question

Plss help me do this​

Answer 1

x1 = -5

x2 = 3

Explanation:

You have the following equation:

`(6)/(x)-(4)/(5)=(2x)/(5)` (1)

To find the solutions of the equation (1) you first eliminate the denominators of the equation, by multiplying the m.c.m, which is 5x, as follow:

`30-4x=2x^2`

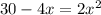
Next, you write the previous equation in the general form ax^2 +bx+c=0, as follow:

`2x^2+4x-30=0`

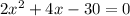
Next, you use the quadratic formula to find the solutions:

`x_(1,2)=(-b\pm √(b^2-4(a)(c)))/(2a)\\\\a=2;\ \ b=4;\ \ c=-30\\\\x_(1,2)=(-4\pm √(4^2-4(2)(-30)))/(2(2))\\\\x_(1,2)=(-4\pm16)/(4)\\\\x_1=-5\\\\x_2=3`

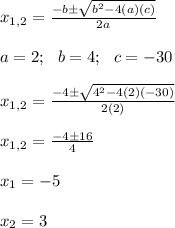
Then, the solutions for the given equation are x1=-5 and x2=3