Question

The system of equations y = one-fourth x minus 5 and y = negative one-half x minus 3 is shown on the graph below.

Answer 1

Answer: This question doesn't give the the answer choices or show the graph. So this question is incomplete

Explanation:

Answer 2

The question is incomplete! Complete question along with answer and step by step explanation is provided below.

Question:

The system of equations y = one-fourth x minus 5 and y = negative one-half x minus 3 is shown on the graph below.

Which statement is true about the solution to the system of equations? The x-value is between 2 and 3, and the y-value is between –4 and –5. The x-value is between –4 and –5, and the y-value is between 2 and 3. The x-value is between –2 and –3, and the y-value is between 4 and 5. The x-value is between 4 and 5, and the y-value is between –2 and –3.

Answer:

The solution is

`(x, y) = (2,67, -4.33)`

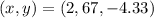
Therefore, the correct statement is

The x-value is between 2 and 3, and the y-value is between –4 and –5.

Explanation:

The given equations are

Equation 1:

`y = (1)/(4)x - 5`

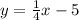
Equation 2:

`y = -(1)/(2)x - 3`

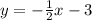
The point of intersection is given by

`(1)/(4)x - 5 = -(1)/(2)x - 3 \\\\(1)/(4)x + (1)/(2)x = 5 - 3 \\\\(3)/(4)x = 2 \\\\x = (2 (4))/(3) \\\\x = (8)/(3) \\\\x = 2.67`

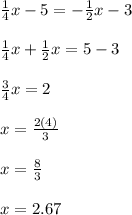
The corresponding y value is

`y = (1)/(4)x - 5 \\\\y = (1)/(4)((8)/(3)) - 5 \\\\y = (2)/(3) - 5 \\\\y = -(13)/(3) \\\\y = -4.33`

So the solution is

`(x, y) = (2,67, -4.33)`

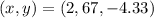
Therefore, the correct statement is

The x-value is between 2 and 3, and the y-value is between –4 and –5.