Question

The sand used for sanding icy roads in the winter is stored in a conical-shaped structure with a radius of 10 m

and a height of 16 m. Calculate the maximum amount of sand which can be stored in this structure.

Answer 1

`V = (1)/(3) (\pi \cdot 10^2 \cdot 16) \\\\V = (1)/(3) (1600 \pi ) \\\\V = 1675.52 \: m^3`

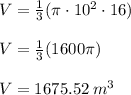
The maximum amount of sand that can be stored in this structure is 1675.52 m³.

Explanation:

The volume of a conical-shaped structure is given by

`V = (1)/(3) (\pi \cdot r^2 \cdot h)`

Where r is the radius and h is the height of the structure.

We are given that

radius = 10m

height = 16m

Substituting the above values into the formula, we get

`V = (1)/(3) (\pi \cdot 10^2 \cdot 16) \\\\V = (1)/(3) (1600 \pi ) \\\\V = 1675.52 \: m^3`

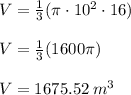
Therefore, the maximum amount of sand th can be stored in this structure is 1675.52 m³.