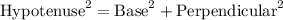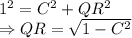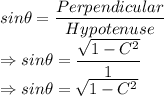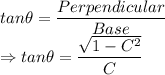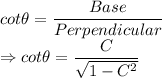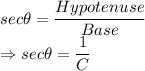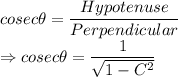Question

suppose for an angle theta in a right triangle cos theta = C. Sketch and label this triangle, and then use it to write the other five trig functions of theta in terms of C.

Answer 1

`sin\theta = √(1-C^2)`

`tan\theta = (√(1-C^2))/(C)`

`cot\theta = (C)/(√(1-C^2))`

`sec\theta = (1)/(C)}`

`cosec\theta = (1)/(√(1-C^2))`

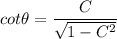
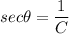
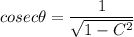
Explanation:

Given that:

`\theta` is an angle in a right angled triangle.

and
`cos\theta = C`

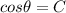
To find:

To draw the triangle and write other five trigonometric functions in terms of C.

Solution:

We know that cosine of an angle is given by the formula:

`cosx =(Base)/(Hypotenuse)`

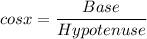
Here, we are given that
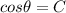`cos\theta = C` OR

`cos\theta = (C)/(1)`

i.e. Base = C and Hypotenuse of triangle = 1

Please refer to the right angled triangle as per given statements.

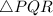`\triangle PQR`, with base PR = C units

and hypotenuse, QP = 1 unit

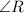`\angle R` is the right angle.

Let us use pythagorean theorem to find the value of perpendicular.

According to pythagorean theorem:

`\text{Hypotenuse}^(2) = \text{Base}^(2) + \text{Perpendicular}^(2)`

`1^(2) = C^(2) + QR^(2)\\\Rightarrow QR = \sqrt {1-C^2}`

`sin\theta = (Perpendicular)/(Hypotenuse)\\\Rightarrow sin\theta = (√(1-C^2))/(1)\\\Rightarrow sin\theta = √(1-C^2)`

`tan\theta = (Perpendicular)/(Base)\\\Rightarrow tan\theta = (√(1-C^2))/(C)`

`cot\theta = (Base)/(Perpendicular)\\\Rightarrow cot\theta = (C)/(√(1-C^2))`

`sec\theta = (Hypotenuse)/(Base)\\\Rightarrow sec\theta = (1)/(C)}`

`cosec\theta = (Hypotenuse)/(Perpendicular)\\\Rightarrow cosec\theta = (1)/(√(1-C^2))`