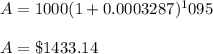Question

a sum of 1000 invested at an jntrest rate 12% per year. Find the amounts in the account after 3 years if intrest is compounded annualy, semiannually, quarerterly, monthly, and daily.

Answer 1

Given Information:

Annual interest rate = r = 12%

Principal amount = P = $1000

Number of years = t = 3

Required Information

Accumulated amount = A = ?

Answer:

Annual compounding = A = $1404.93

Semi-annuall compounding = A = $1418.52

Quarterly compounding = A = $1425.76

Monthly compounding = A = $1432.30

Daily compounding = A = $1433.14

Explanation:

The accumulated amounts in terms of compound interest is given by

`A = P(1 + i)^N`

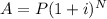
Where P is the initial amount invested and A is the accumulated amount.

For annual compounding:

i = 0.12

N = 3

`A = 1000(1 + 0.12)^3 \\\\A = \$ 1404.93`

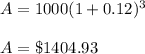
For semiannually compounding:

i = 0.12/2 = 0.06

N = 2*3 = 6

`A = 1000(1 + 0.06)^6 \\\\A = \$ 1418.52`

For quarerterly compounding:

i = 0.12/4 = 0.03

N = 4*3 = 12

`A = 1000(1 + 0.03)^12 \\\\A = \$ 1425.76`

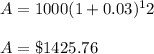
For monthly compounding:

i = 0.12/30 = 0.004

N = 30*3 = 90

`A = 1000(1 + 0.004)^90 \\\\A = \$ 1432.30`

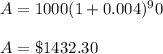
For daily compounding:

i = 0.12/365 = 0.0003287

N = 365*3 = 1095

`A = 1000(1 + 0.0003287)^1095 \\\\A = \$ 1433.14`