Question

The temperature over a 9​-hour period is given by Upper T (t )equalsnegative t squared plus 4 t plus 34. ​(a) Find the average temperature. ​(b) Find the minimum temperature. ​(c) Find the maximum temperature.

Answer 1

(a) 25 degrees

(b) -11 degrees

(c) 38 degrees

Explanation:

The temperature function is:

`T(t) = -t^2+4t+34`

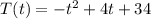
(a) The average value for a temperature is:

`M=(1)/(b-a)* \int\limits^b_a {f(x)} \, dx`

In this particular case, the average temperature is:

`M=(1)/(9-0)* \int\limits^9_0 {T(t)} \, dt \\M=(1)/(9)* \int\limits^9_0 {(-t^2+4t+34)} \, dt \\M=(1)/(9)* {(-(t^3)/(3)+2t^2+34t)}|_0^9\\M=(1)/(9)*( {(-(9^3)/(3)+2*(9^2)+34*9)-0)`

`M=25`

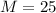
The average temperature is 25 degrees.

(b) The expression is a parabola that is concave down, therefore there are no local minimums, which means that the minimum temperature will be at one of the extremities of the interval:

`T(0) = -0^2+4*0+34=34\\T(9) = -9^2+9*4+34=-11`

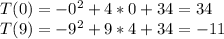
The minimum temperature is -11 degrees.

(c) The maximum temperature will occur at the point for which the derivate of the temperature function is zero:

`T(t) = -t^2+4t+34\\T'(t)=-2t+4=0\\2t=4\\t=2`

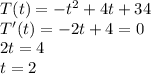
At t = 2, the temperature is:

`T(2) = -2^2+4*2+34=38`

The maximum temperature is 38 degrees.