Question

Added to Six Flags St. Louis in the Colossus is a giant Ferris wheel. Its diameter is 165 feet, it rotates at a rate of about 1.6 revolutions per minute, and the bottom of the wheel is 15 feet above the ground. Determine an equation that relates a rider's height above the ground at time . Assume the passenger begins the ride at the bottom of the wheel.

Answer 1

The height of the rider as a function of time is
`h(t) = 15 + 82.5\cdot (1-\cos 0.168t) \,[ft]`, where time is measured in seconds.

Explanation:

Given that Ferris wheel rotates at constant rate and rider begins at the bottom of the wheel, the height of the rider as a function of time is modelled after this expression:

`h(t) = h_(bottom) + (1-\cos \omega t)\cdot r_(w)`

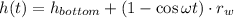
Where:

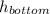`h_(bottom)` - Height of the bottom with respect to ground, measured in feet.

`\omega` - Angular speed of the ferris wheel, measured in radians per second.

`t` - Time, measured in seconds.

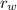`r_(w)` - Radius of the Ferris wheel, measured in feet.

The angular speed of the ferris wheel, measured in radians per second, is obtained from the following expression:

`\omega = (\pi)/(30)\cdot \dot n`

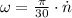
Where:

`\dot n` - Angular speed of the ferris wheel, measured in revolutions per minute.

If
`\dot n = 1.6\,rpm`, then:

`\omega = (\pi)/(30)\cdot (1.6\,rpm)`

`\omega \approx 0.168\,(rad)/(s)`

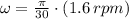
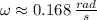
Now, given that
`h_(bottom) = 15\,ft`,
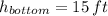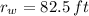`r_(w) = 82.5\,ft` and
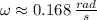`\omega \approx 0.168\,(rad)/(s)`, the height of the rider as a function of time is:

`h(t) = 15 + 82.5\cdot (1-\cos 0.168t) \,[ft]`