Answer:
Vertical asymptote:
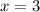
Horizontal asymptote:
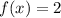
Domain of f(x) is all real numbers except 3.
Range of f(x) is all real numbers except 2.
Explanation:
Given:
Function:
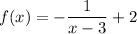
One root,

To find:
Vertical and horizontal asymptote, domain, range and roots of f(x).
Solution:
First of all, let us find the roots of f(x).
Roots of f(x) means the value of x where f(x) = 0
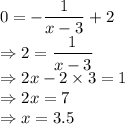
One root,

Domain of f(x) i.e. the values that we give as input to the function and there is a value of f(x) defined for it.
For x = 3, the value of f(x)
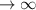
For all, other values of
 ,
,
 is defined.
is defined.
Hence, Domain of f(x) is all real numbers except 3.
Range of f(x) i.e. the values that are possible output of the function.
f(x) = 2 is not possible in this case because something is subtracted from 2. That something is
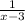 .
.
Hence, Range of f(x) is all real numbers except 2.
Vertical Asymptote is the value of x, where value of f(x)
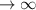 .
.

It is possible only when
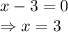
 vertical asymptote:
vertical asymptote:
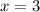
Horizontal Asymptote is the value of f(x) , where value of x
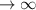 .
.
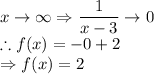
 Horizontal asymptote:
Horizontal asymptote:
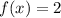
Please refer to the graph of given function as shown in the attached image.