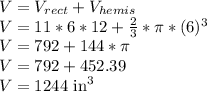Question

What is the volume in cubic inches of the solid figure, rounded to the nearest cubic inch? Do not use units or commas in your answer.

Answer 1

The volume of the figure is approximately 1244 in³

Explanation:

The figure is formed by a rectangular prism and a hemisphere, therefore its total volume is formed by the the sum of the volume of each of these forms. The volume of a rectangular prism can be found by using the expression:

`V_(rect) = length*width*height`

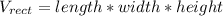
While the volume of a hemisphere is given by:

`V_(hemis) = (2)/(3)*\pi*r^3`

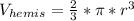
The radius of the hemisphere is the difference between the total length of the figure and the length of the prism, therefore:

`r = 17 - 11 = 6 \text{ in}`

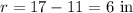
We can now find the volume of the figure:

`V = V_(rect) + V_(hemis)\\V = 11*6*12 + (2)/(3)*\pi*(6)^3\\V = 792 + 144*\pi\\V = 792 + 452.39\\V = 1244 \text{ in}^3`