Answer:
The formula that represents the length of an equilateral triangle’s side (s) in terms of the triangle's area (A) is
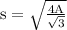 .
.
Explanation:
We are given the area of an Equilateral triangle which is A =
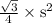 . And we have to represent the length of an equilateral triangle’s side (s) in terms of the triangle's area (A).
. And we have to represent the length of an equilateral triangle’s side (s) in terms of the triangle's area (A).
So, the area of an equilateral triangle =
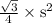
where, s = side of an equilateral triangle
A =
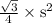
Cross multiplying the fractions we get;
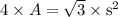
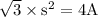
Now. moving
 to the right side of the equation;
to the right side of the equation;
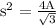
Taking square root both sides we get;
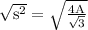
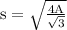
Hence, this formula represents the length of an equilateral triangle’s side (s) in terms of the triangle's area (A).