Question

The marginal cost (dollars) of printing a poster when x posters have been printed is given by the following equation. C'(x)=x^-3/4 Find the cost of printing 142 more posters when 18 have already been printed.

The cost of printing 142 more posters when 18 have already been printed is $________.
(Round to the nearest cent as needed.)

Answer 1

The cost of printing 142 more posters when 18 has already been printed is $5.57.

Explanation:

We are given that the marginal cost (dollars) of printing a poster when x posters have been printed is given by the following equation C'(x)=x^-3/4.

The given equation is:
`C'(x) = x^{(-3)/(4) }`

The cost of printing 142 more posters when 18 have already been printed is given by;

Integrating both sides of the equation and using the limits we get;

`\int_(a)^(b) C'(x) dx=\int_(18)^(142) x^{(-3)/(4)}dx`

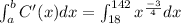
As we know that
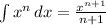`\int\limits {x}^(n) \, dx = (x^(n+1) )/(n+1)` , so;

=
`\frac{x^{(-3)/(4)+1 } }{(-3)/(4)+1 } ]^(142) __1_8`

=
`\frac{x^{(1)/(4) } }{(1)/(4) } ]^(142) __1_8`

=
`4[x^{(1)/(4) } } ]^(142) __1_8`

=
`4[(142)^{(1)/(4) }- (18)^{(1)/(4) }} ]`

= $5.57

Hence, the cost of printing 142 more posters when 18 has already been printed is $5.57.