Answer:
The best option is B: X' = (-7,-4), Y' = (-2,6), Z'=(8, 3).
Explanation:
Each vertex can be represented as a vector with regard to origin.
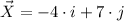 ,
,
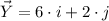 and
and
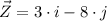 .
.
The magnitudes and directions of each vector are, respectively:
X:
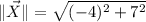
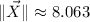
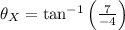
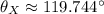
Y:
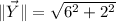
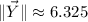
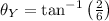
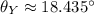
Z:
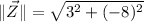
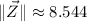
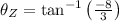
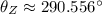
Now, the rotation consist is changing the direction of each vector in
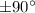 , which means the existence of two solutions. That is:
, which means the existence of two solutions. That is:
![\vec p = r \cdot [\cos (\theta \pm 90^(\circ))\cdot i + \sin (\theta \pm 90^(\circ))\cdot j]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ed8swkaldjirkq5bfihl39udc2m740t7if.png)
Where
 and
and
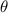 are the magnitude and the original angle of the vector.
are the magnitude and the original angle of the vector.
Solution I (
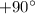 )
)
![\vec p_(X) = 8.063\cdot [\cos (119.744^(\circ)+90^(\circ))\cdot i + \sin (119.744^(\circ)+90^(\circ))\cdot j]](https://img.qammunity.org/2021/formulas/mathematics/high-school/hwyljiyjmgabl7y9f3hzmh6v94f16f22nv.png)
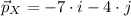
![\vec p_(Y) = 6.325\cdot [\cos(18.435^(\circ)+90^(\circ))\cdot i+\sin(18.435^(\circ)+90^(\circ))\cdot j]](https://img.qammunity.org/2021/formulas/mathematics/high-school/u4olnju78dbqfy8tfzy1vdq609qtfxtuvl.png)
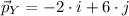
![\vec p_(Z) = 8.544\cdot [\cos(290^(\circ)+90^(\circ))\cdot i +\sin(290^(\circ)+90^(\circ))\cdot j]](https://img.qammunity.org/2021/formulas/mathematics/high-school/pkilwft6epd4291vka8pqwd3v57npbvyre.png)
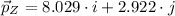
Solution II (
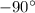 )
)
![\vec p_(X) = 8.063\cdot [\cos (119.744^(\circ)-90^(\circ))\cdot i + \sin (119.744^(\circ)-90^(\circ))\cdot j]](https://img.qammunity.org/2021/formulas/mathematics/high-school/d4v7sqlshjfa1lttwjygtbp69avlt1rtrr.png)
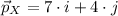
![\vec p_(Y) = 6.325\cdot [\cos(18.435^(\circ)-90^(\circ))\cdot i+\sin(18.435^(\circ)-90^(\circ))\cdot j]](https://img.qammunity.org/2021/formulas/mathematics/high-school/dfmjejlx2qur2huwy5i3dbzsen4617ro0g.png)
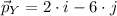
![\vec p_(Z) = 8.544\cdot [\cos(290^(\circ)-90^(\circ))\cdot i +\sin(290^(\circ)-90^(\circ))\cdot j]](https://img.qammunity.org/2021/formulas/mathematics/high-school/qmwzuxt2tz5m6ry9uo8az4x05tjr6gruhe.png)
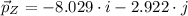
The rotated vertices are: i) X' = (-7,-4), Y' = (-2,6), Z'=(8.029, 2.922) or ii) X' = (7,4), Y' = (2,-6), Z' = (-8.029, -2.922). The best option is B: X' = (-7,-4), Y' = (-2,6), Z'=(8, 3).