Question

Suppose Hillard Manufacturing sold an issue of bonds with a 10-year maturity, a $1,000 par value, a 10% coupon rate, and semiannual interest payments.

a. Two years after the bonds were issued, the going rate of interest on bonds such as these fell to 6%. At what price would the bonds sell?
b. Suppose that 2 years after the initial offering, the going interest rate had risen to 12%. At what price would the bonds sell?
c. Suppose that 2 years after the issue date (as in part a) interest rates fell to 6%. Suppose further that the interest rate remained at 6% for the next 8 years. What would happen to the price of the bonds over time?

Answer 1

A) Market Value: $1,251.2220

B) Market Value: $898.94

C) the price of the bonds will decrease over time. As the nominal amount will suffer from less discounting over time at maturity will match the nominal amount of $ 1,000. To do so It need to decrease over time.

Step-by-step explanation:

The value of the bonds will be the present value of the future coupon payment and maturity at the new rate of 6%

PV of the coupon payment

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

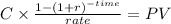
C 50.000 (1,000 x 10% / 2 ayment per year)

time 16 (8 year to maturity x 2 payment per year)

rate 0.03 (6% over two payment per year)

`50 * (1-(1+0.03)^(-16) )/(0.03) = PV\\`

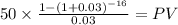
PV $628.0551

PV of the maturity

`(Maturity)/((1 + rate)^(time) ) = PV`

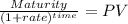
Maturity 1,000.00

time 16.00

rate 0.03

`(1000)/((1 + 0.03)^(16) ) = PV`

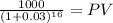
PV 623.17

PV c $628.0551

PV m $623.1669

Total $1,251.2220

If the rate is 12%

PV of the coupon payment:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

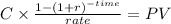
C 50.000

time 16

rate 0.06

`50 * (1-(1+0.06)^(-16) )/(0.06) = PV\\`

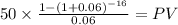
PV $505.2948

PV of the maturity:

`(Maturity)/((1 + rate)^(time) ) = PV`

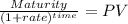
Maturity 1,000.00

time 16.00

rate 0.06

`(1000)/((1 + 0.06)^(16) ) = PV`

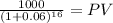
PV 393.65

PV c $505.2948

PV m $393.6463

Total $898.9410