Question

Determine if the vector u is in the column space of matrix A and whether it is in the null space of A.

u = -4 A = 1 0 3
-5 -2 -1 -4
3 3 -3 0
1 -1 3 6
A) In Col A, not in Nul A
B) Not in Col A, not in Nul A
C) In Col A and in NulA
D) Not in Col in Nul A

Answer 1

The question asks about the relationship between vector u and matrix A's column and null spaces. To answer, we must check if u is a linear combination of A's columns and if Au equals the zero vector.

Step-by-step explanation:

The question pertains to determining the relationships between a given vector u and the column space and null space of matrix A. To decide if vector u is in the column space of A, we need to see if u can be expressed as a linear combination of the columns of A. On the other hand, vector u is in the null space of matrix A if Au = 0, where 0 is the zero vector with the same number of rows as A.

When vectors A and B are equal in magnitude and opposite in direction, the vector difference A - B will point in the same direction as vector A (and opposite the direction of vector B) because the subtraction of a vector that is in the opposite direction effectively doubles the magnitude in the direction of vector A.

Answer 2

Answer: d) Not in Col in Nul A

Step-by-step explanation: The definition of Column Space of an m x n matrix A is the set of all possible combinations of the columns of A. It is denoted by col A. To determine if a vector is a column space, solve the matrix equation:

A.x = b or, in this case,
`A.x=u`.

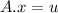To solve, first write the augmented matrix of the system:

`\left[\begin{array}{cccc}1&0&3&-4\\-2&-1&-4&-5\\3&-3&0&3\\-1&3&6&1\end{array}\right]`

Now, find the row-echelon form of matrix A:

1) Multiply 1st row by 2 and add 2nd row;

2) Multiply 1st row by -3 and add 3rd row;

3) MUltiply 1st row by 1 and add 4th row;

4) MUltiply 2nd row by -1;

5) Multiply 2nd row by 3 and add 3rd row;

6) Multiply 2nd row by -3 and add 4th row;

7) Divide 3rd row by -15;

8) Multiply 3rd row by -15 and add 4th row;

The echelon form matrix will be:

`\left[\begin{array}{cccc}1&0&3&-4\\0&1&-2&13\\0&0&1&-(51)/(15)\\0&0&0&-13 \end{array}\right]`

Which gives a system with impossible solutions.

But if
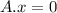`A.x=0`, there would be a solution.

Null Space of an m x n matrix is a set of all solutions to
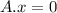`A.x=0`, so vector u is a null space of A, denoted by null (A)