Question

A life insurance company sells a $100,000 one year term life insurance policy to a 30-year old male for $475. The probability that the male survives the year is .999172. Find the expected value for the insurance company.

Answer 1

The expected value for the insurance company is $392.20.

Explanation:

The expected value of a random variable, X is:

`E(X)=x\cdot P(X)`

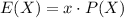
It is provided that a life insurance company sells a $100,000 one year term life insurance policy to a 30-year old male for $475.

The probability that the male survives the year is, P(S) = 0.999172.

Then the probability that the male does not survives the year is:

P (S') = 1 - P (S)

= 1 - 0.999172

P (S') = 0.000828

The amount the company owes the male if he survives is, S = $475.

The amount the company owes the male if he does not survives is,

S' = $475 - $100,000 = -$99525.

Compute the expected value for the insurance company as follows:

`E(\text{Insurance Company})=S\cdot P(S)+S'\cdot P(S')`

`=(475* 0.999172)+(-99525* 0.000828)\\=474.6067-82.4067\\=392.20`

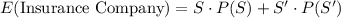
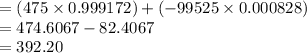
Thus, the expected value for the insurance company is $392.20.