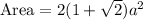Question

A regular octagon is inscribed inside a circle. The perimeter of the octagon is units. A: What is the measure of a side of the octagon? B: What is the measure of a central angle of the octagon? C: What is the approximate measure of the apothem of the octagon (to the nearest hundredth of a unit)? D: Using your answer to part C, what is the approximate area of the octagon (to the nearest whole )?

Answer 1

Explained below.

Explanation:

Consider the diagram of a regular octagon is inscribed inside a circle.

Suppose the perimeter if the octagon is 8a.

(a)

Compute the measure of a side of the octagon as follows:

`\text{Perimeter}=8* side\\\\8* side=8a\\\\side=a`

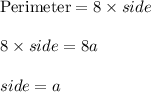
Thus, the side of the octagon is a units.

(b)

The sum of all angles of around a point is 360°.

Consider the point P on the octagon.

The sum of all the angle surrounding P will be 360°.

There are a total of 8 angle surrounding the point P.

Then the measure of central angle is:

`\text{Central Angle}=(360^(o))/(8)=45^(o)`

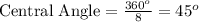
Thus, the measure of central angle is 45°.

(c)

The line segment from the center of an octagon to the midpoint of a side, perpendicular to said side, is known as the apothem.

Consider the diagram.

In the diagram the line segment PC is an apothem, that is perpendicular to the AB.

The measure of segment AC = a/2 and the measure of segment PA is r (radius of the circle).

Compute he measure of PC as follows:

`PA^(2)=PC^(2)+AC^(2)\\\\PC^(2)=PA^(2)-AC^(2)\\\\PC=\sqrt{PA^(2)-AC^(2)}`

`=\sqrt{r^(2)-(a^(2))/(4)}`

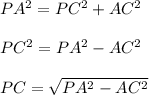
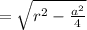
Thus, the measure of the apothem of the octagon is
`\sqrt{r^(2)-(a^(2))/(4)}`.

(d)

The area of an octagon is:

`\text{Area}=2(1+√(2))a^(2)`