Question

Suppose the preliteracy scores of three-year-old students in the United States are normally distributed. Shelia, a preschool teacher, wants to estimate the mean score on preliteracy tests for the population of three-year-olds. She draws a simple random sample of 20 students from her class of three-year-olds and records their preliteracy scores (in points).

81,84,87,91,91,91,92,92,94,95,97,99,100,102,106,107,107,111,115,116
1. Calculate the sample mean (x⎯⎯⎯), sample standard deviation (????), and standard error (SE) of the students' scores. Round your answers to four decimal places.
2. Determine the ????-critical value (????) and margin of error (m) for a 99% confidence interval. Round your answers to three decimal places.
3. What are the lower and upper limits of a 99% confidence interval? Round your answers to three decimal places.
4. Which is the correct interpretation of the confidence interval?
a. Shelia is certain that the true population mean is between 91.537 points and 104.263 points.
b. Shelia is 99% confident that the true population mean is between 92.171 points and 103.629 points.
c. There is a 99% chance that the true population mean is between 92.171 points and 103.629 points.
d. Shelia is 99% confident that the true population mean is between 91.537 points and 104.263 points.
e. There is a 99% chance that the population mean is between 91.537 points and 104.263 points.

Answer 1

Answer: 1. sample mean = 97.7; sample standard deviation(s) = 9.9467; standard error (SE) = 2.2241

2. t-critical value = 2.861; margin of error (m) = 97.9 ± 6.363

3. Lower limits = 91.537; upper limit = 104.263

4. d. Sheila is 99% confident that the true population mean is between 91.537 points and 104.263 points.

Step-by-step explanation: Knowing that this sample has 20 individuals, which means n = 20:

1. Sample mean is the average of the data set:

mean =
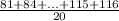`(81+84+...+115+116)/(20)` = 97.9

Sample standard deviation is the spread of the sample data set from the mean:

s =
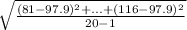`\sqrt{((81-97.9)^(2)+...+(116-97.9)^(2))/(20-1) }` = 9.9467

Standard Error shows how far the mean of the set is from the true popultaion mean:

SE =
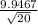`(9.9467)/(√(20) )` = 2.2241

2. The t-critical value (t) is the value you use to decide if you reject or accept the null hypothesis. It can be calculated by a calculator or found in the t-test table. To use the table:

Degrees of freedom for this set is: n - 1 = 19

Critical value (α) = 0.99. For the t-test:
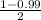`(1-0.99)/(2)` = 0.005

`t_(19,0.005)` = 2.861

Margin of error (m) shows, in percentage, how different your results are from the real population value. It is calculated as:

m = 97.9 ± 2.861*2.2241 = 97.9 ± 6.363

3. Lower and Upper limits are the interval the true mean can assume with a determined certainty.

lower limit = 97.9 - 6.363 = 91.537

upper limit = 97.9 + 6.363 = 104.263

4. In this case, the statistics shows that the true population mean is between 91.537 and 104.263, 99% of the time.