Answer:
The sequence diverges ( B )
Step-by-step explanation:
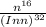
Applying the Growth rates of sequences theorem to find the limit of the given sequence above
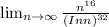 = ∞ this means that
= ∞ this means that
The sequence is divergent because the rate at which n increase is very much higher than the rate at which (In n) increases