Question

In the far future, astronauts travel to the planet Saturn and land on Mimas, one of its 62 moons. Mimas is small compared with the Earth's moon, with mass Mm = 3.75 ✕ 1019 kg and radius Rm = 1.98 ✕ 105 m, giving it a free-fall acceleration of g = 0.0636 m/s2. One astronaut, being a baseball fan and having a strong arm, decides to see how high she can throw a ball in this reduced gravity. She throws the ball straight up from the surface of Mimas at a speed of 41 m/s (about 91.7 mph, the speed of a good major league fastball).

(a) Predict the maximum height of the ball assuming g is constant and using energy conservation. Mimas has no atmosphere, so there is no air resistance.
(b) Now calculate the maximum height using universal gravitation.
(c) How far off is your estimate of part (a)? Express your answer as a percent difference and indicate if the estimate is too high or too low.

Answer 1

a) h = 13,205.4 m

b) r_f = 2.12 106 m

c) e% = 0.68%

Step-by-step explanation:

a) This is an exercise we are asked to use energy conservation,

Starting point. On the surface of Mimas

Em₀ = K = ½ m v²

Final point. Where the ball stops

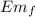`Em_(f)` = U = m g h

Em₀ = Em_{f}

½ m v² = m g h

h = ½ v² / g

let's calculate

h = ½ 41² / 0.0636

h = 13,205.4 m

b) For this part we are asked to use the law of universal gravitation, write the energy

starting point. Satellite surface

Em₀ = K + U = ½ m v² - GmM / r_o

final point. Where the ball stops

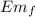`Em_(f)`= U = - G mM / r_f

Em₀ = Em_{f}

½ m v² - G m M / r_o = - G mM / r_f

In this case all distances are measured from the center of the satellite

1 / rf = 1 / GM (-½ v² + G M / r_o)

let's calculate

1 / rf = 1 / (6.67 10⁻¹¹ 3.75 10¹⁹) (- ½ 41 2 + 6.67 10⁻¹¹ 3.75 10¹⁹ / 1.98 105)

1 / r_f = 3,998 10⁻¹¹(-840.5 + 12.63 10³)

1 / r_f = 4,714 10⁻⁷

r_f = 1 / 4,715 10⁻⁷

r_f = 2.12 106 m

to measure this distance from the satellite surface

r_f ’= r_f - r_o

r_f ’= 2.12 106 - 1.98 105

r_f ’= 1,922 106 m

c) the percentage difference is

e% = 13 205.4 / 1,922 106 100

e% = 0.68%

The estimate of part a is a little low