Question

Write each of the following expressions without using absolute value.

|a−7|−|a−9|, if a<7
PLEASE HELP!!!! D:

Answer 1

Answer: -2

=======================================================

If a < 7, then |a-7| = -(a-7) = -a+7 based on how absolute value functions are constructed. We're using the idea that

`|x-k| = \begin{cases}x-k \ \text{ if } \ x \ge k\\ -(x-k) \ \text{ if } \ x < k\end{cases}`

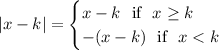
Also, if a < 7, then |a-9| = -(a-9) = -a+9. This is true whenever 'a' is less than 9 for similar reasoning as above.

---------

So we have,

|a-7| - |a-9| = -a+7 - (-a+9) = -a+7+a-9 = -2

As long as a < 7, the result of |a-7| - |a-9| will always be -2.

---------

As an example, let's say a = 0

|a-7| - |a-9| = |0-7| - |0-9|

|a-7| - |a-9| = |-7| - |-9|

|a-7| - |a-9| = 7 - 9

|a-7| - |a-9| = -2

I recommend you try out other values of 'a' to see if you get -2 or not. Of course only pick values that are smaller than 7.