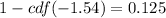Question

Your PI claims that the proportion of Morpho butterflies in a population that are blue is 0.3 .A sample is independently obtained from this population. Of 200 sampled Morphos, 50 turn out to be blue.Given only this information, carry out a hypothesis test to evaluate the claim. What is closest to the p-value that you obtain?

Answer 1

Complete Question

Your PI claims that the proportion of Morpho butterflies in a population that are blue is 0.3 .A sample is independently obtained from this population. Of 200 sampled Morphos, 50 turn out to be blue.Given only this information, carry out a hypothesis test to evaluate the claim. What is closest to the p-value that you obtain?

A 0.019

B 0.038

C 0.070

D 0.139

Answer:

The correct answer is D

Explanation:

From the question we are told that

The population proportion of blue butterflies is
`p = 0.3`

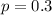
The sample size is
`n = 200`

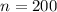
The sample mean is
`\= x = 50`

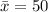
The Null Hypothesis is mathematically represented as

`H_o : p = 0.3`

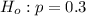
The Alternative Hypothesis is mathematically represented as

`H_a : p \\e 0.3`

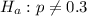
Now the sample proportion is mathematically represented as

`\r p = (\= x)/(n)`

substituting values

`\r p = (50 )/(200 )`

`\r p = 0.25`

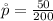
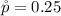
Generally the test statistics is mathematically represented as

`z = \frac{\r p - p }{\sqrt{(p(1-p))/(n ) } }`

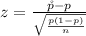
substituting values

`z = \frac{ 0.25 - 0.3 }{\sqrt{(0.3(1-0.3))/(200 ) } }`

`z = -1.54`

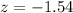
The p-value for a two-tailed test is mathematically represented as

for lower -tail test

`p-value = P(Z \le z | H0\ is \ true) = cdf(z )`

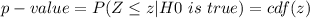
for higher-tail test

`p-value = P(Z \ge z | H0\ is \ true) = 1- cdf(z )`

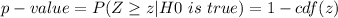
for this test i assumed a 0.05 level of significance

Now

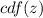`cdf(z)` is the cumulative distribution function for test statistics under the null hypothesis

Which can be calculated using MInitab (A statistics calculator )

for lower-tail test

The p-value is not significant

for higher-tail test

p-value is

`1- cdf(-1.54) = 0.125`