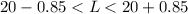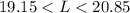Answer:
The 90% confidence level is
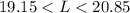
Explanation:
From the question we are told that
The sample size is
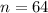
The mean age is

The standard deviation is
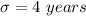
Generally the degree of freedom for this data set is mathematically represented as
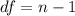
substituting values
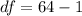
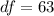
Given that the level of confidence is 90% the significance level is mathematically evaluated as
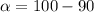
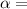 10 %
10 %
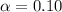
Now

Since we are considering a on tail experiment
The critical value for half of this significance level at the calculated degree of freedom is obtained from the critical value table as
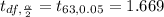
The margin for error is mathematically represented as
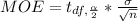
substituting values
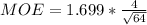
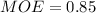
he 90% confidence interval for the true average age of all students in the university is evaluated as follows
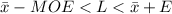
substituting values