Answer:
The rotor of the gas turbine rotates 12250 revolutions before coming to rest.
Step-by-step explanation:
Given that rotor of gas turbine is decelerating at constant rate, it is required to obtained the value of angular acceleration as a function of time, as well as initial and final angular speeds. That is:
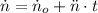
Where:
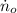 - Initial angular speed, measured in revolutions per minute.
- Initial angular speed, measured in revolutions per minute.
 - Final angular speed, measured in revolutions per minute.
- Final angular speed, measured in revolutions per minute.
 - Time, measured in minutes.
- Time, measured in minutes.
 - Angular acceleration, measured in revoiutions per square minute.
- Angular acceleration, measured in revoiutions per square minute.
The angular acceleration is now cleared:
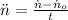
If
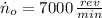 ,
,
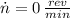 and
and
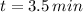 , the angular acceleration is:
, the angular acceleration is:
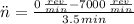
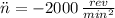
Now, the final angular speed as a function of initial angular speed, angular acceleration and the change in angular position is represented by this kinematic equation:
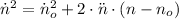
Where
 and
and
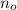 are the initial and final angular position, respectively.
are the initial and final angular position, respectively.
The change in angular position is cleared herein:

If
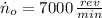 ,
,
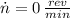 and
and
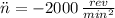 , the change in angular position is:
, the change in angular position is:
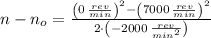
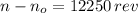
The rotor of the gas turbine rotates 12250 revolutions before coming to rest.