Answer:
The probability is
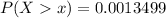
Explanation:
From the question we are told that
The mean is
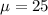
The standard deviation is
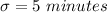
The random number
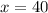
Given that the time taken is normally distributed the probability is mathematically represented as
![P(X > x) = P[(X -\mu)/(\sigma ) > (x -\mu)/(\sigma ) ]](https://img.qammunity.org/2021/formulas/mathematics/college/3y4xga3l2vldc07xisv6x99pwrvce2e9de.png)
Generally the z-score for the normally distributed data set is mathematically represented as
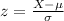
So
![P(X > x) = P[Z > (40 -25)/(5 ) ]](https://img.qammunity.org/2021/formulas/mathematics/college/oeilqnu4z2di5rnugsbe6e64d0cbzy3yxr.png)
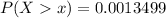
This value is obtained from the z-table