Question

Monica’s school band held a car wash to raise money for a trip to a parade in New York City. After washing 125 cars, they made $775 from a combination of $5.00 quick washes and $8.00 premium washes. This system of equations models the situation. x + y =125 5x + 8y = 775

Answer 1

`x+y = 125` (1)

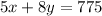`5x+8y = 775` (2)

We can solve for y from equation (1) and we got:

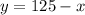`y = 125-x` (3)

And replacing (3) into (2) we got:

`5x +8(125-x) = 775`

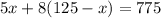
And solving for x we got:

`1000-3x = 775`

`3x= 225`

`x=75`

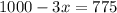
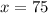
And solving for y from (3) we got:

`x= 125-75 =50`

And the solution would be x = 50 and y =75

Explanation:

For this problem we have the following system of equations:

`x+y = 125` (1)

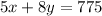`5x+8y = 775` (2)

We can solve for y from equation (1) and we got:

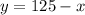`y = 125-x` (3)

And replacing (3) into (2) we got:

`5x +8(125-x) = 775`

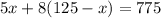
And solving for x we got:

`1000-3x = 775`

`3x= 225`

`x=75`

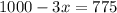
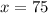
And solving for y from (3) we got:

`x= 125-75 =50`

And the solution would be x = 50 and y =75