Question

The magnetic field in a cyclotron is 1.25 T, and the maximum orbital radius of the circulating protons is 0.40 m. (a) What is the kinetic energy of the protons when they are ejected from the cyclotron

Answer 1

1.92 x 10⁻¹²J

Step-by-step explanation:

The magnetic force from the magnetic field gives the circulating protons gives the particle the necessary centripetal acceleration to keep it orbiting round the circular path. And from Newton's second law of motion, the force(F) is equal to the product of the mass(m) of the proton and the centripetal acceleration(a). i.e

F = ma

Where;

a =
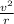`(v^2)/(r)` [v = linear velocity, r = radius of circular path]

=> F = m
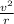`(v^2)/(r)` ------------(i)

We also know that the magnitude of this magnetic force experienced by the moving charge (proton) in a magnetic field is given by;

F = q v B sin θ ----------(ii)

Where;

q = charge of the particle

v = velocity of the particle

B = magnetic field

θ = the angle between the velocity and the magnetic field.

Combining equations (i) and (ii) gives

m
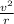`(v^2)/(r)` = q v B sin θ [θ = 90° since the proton is orbiting at the maximum orbital radius]

=> m
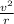`(v^2)/(r)` = q v B sin 90°

=> m
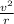`(v^2)/(r)` = q v B

Divide both side by v;

=> m
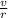`(v)/(r)` = qB

Make v subject of the formula

v =
`(qBr)/(m)`

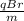
From the question;

B = 1.25T

m = mass of proton = 1.67 x 10⁻²⁷kg

r = 0.40m

q = charge of a proton = 1.6 x 10⁻¹⁹C

Substitute these values into equation(iii) as follows;

v =
`((1.6*10^(-19))(1.25)(0.4))/((1.67*10^(-27)))`

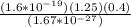
v = 4.79 x 10⁷m/s

Now, the kinetic energy, K, is given by;

K =
`(1)/(2)`mv²

m = mass of proton

v = velocity of the proton as calculated above

K =
`(1)/(2)(1.67*10^(-27) * (4.79 * 10^7)^2 )`

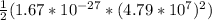
K = 1.92 x 10⁻¹²J

The kinetic energy is 1.92 x 10⁻¹²J