Question

Determine the area under the standard normal curve that lies between â(a) Upper Z equals negative 0.12Z=â0.12 and Upper Z equals 0.12Z=0.12â, â(b) Upper Z equals negative 0.35Z=â0.35 and Upper Z equals 0Z=0â, and â(c) Upper Z equals 0.02Z=0.02 and Upper Z equals 0.82Z=0.82. â(a) The area that lies between Upper Z equals negative 0.12Z=â0.12 and Upper Z equals 0.12Z=0.12 is nothing. â(Round to four decimal places asâ needed.) â(b) The area that lies between Upper Z equals negative 0.35Z=â0.35 and Upper Z equals 0Z=0 is nothing. â(Round to four decimal places asâ needed.) â(c) The area that lies between Upper Z equals 0.02Z=0.02 and Upper Z equals 0.82Z=0.82 is nothing

Answer 1

The answer is below

Explanation:

The z score is a measure used in statistic to determine the number of standard deviations by which the raw score is above or below the mean. . The z score is given by:

`z=(x-\mu)/(\sigma)\\ where\ \mu \ is \ the\ mean, \sigma\ is\ the\ standard\ deviation\ and\ x \ is\ the\ raw\ score`

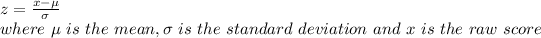
(a) Z = -0.12 and Z = 0.12

From the normal distribution table, Area between z equal -0.12 and z equal 0.12 = P(-0.12 < z < 0.12) = P(z < 0.12) - P(z < -0.12) = 0.5478 - 0.4522 = 0.0956 = 9.56%

b) The area that lies between Z = - 0.35 and Z=0

From the normal distribution table, Area between z equal -0.35 and z equal 0 = P(-0.35 < z < 0) = P(z < 0) - P(z < -0.35) = 0.5 - 0.3594 = 0.1406 = 14.06%

c) The area that lies between Z = 0.02 and Z = 0.82

From the normal distribution table, Area between z equal 0.02 and z equal 0.82 = P(0.02 < z < 0.82) = P(z < 0.82) - P(z < 0.02) = 0.7939 - 0.5080 = 0.2859 = 28.59%