Question

A solid non-conducting sphere of radius R carries a charge Q1 distributed uniformly. The sphere is surrounded by a concentric spherical shell of inner radius Ra and outer radius Rb . The shell carries a total charge Q2 distributed uniformly in its volume. What is the net electric field at a radial distance r such that R < r < Ra

Answer 1

E = k Q₁ / r²

Step-by-step explanation:

For this exercise that asks us for the electric field between the sphere and the spherical shell, we can use Gauss's law

Ф = ∫ E .dA =
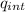`q_(int)` / ε₀

where Ф the electric flow, qint is the charge inside the surface

To solve these problems we must create a Gaussian surface that takes advantage of the symmetry of the problem, in this almost our surface is a sphere of radius r, that this is the sphere of and the shell, bone

R <r <R_a

for this surface the electric field lines are radial and the radius of the sphere are also, therefore the two are parallel, which reduces the scalar product to the algebraic product.

E A = q_{int} /ε₀

The charge inside the surface is Q₁, since the other charge Q₂ is outside the Gaussian surface, therefore it does not contribute to the electric field

q_{int} = Q₁

The surface area is

A = 4π r²

we substitute

E 4π r² = Q₁ /ε₀

E = 1 / 4πε₀ Q₁ / r²

k = 1/4πε₀

E = k Q₁ / r²