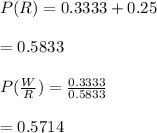Answer:
Following are the answer to this question:
Explanation:
In the question first calls the W if the transmitted chip was white so, the W' transmitted the chip is red or R if the red chip is picked by the urn II.
whenever a red chip is chosen from urn II, then the probability to transmitters the chip in white is:

The probability that only the transmitted chip is white is therefore
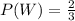 , since urn, I comprise 3 chips and 2 chips are white.
, since urn, I comprise 3 chips and 2 chips are white.
But if the chip is white so, it is possible that urn II has 4 chips and 2 of them will be red since urn II and 2 are now visible, and it is possible to be:
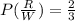
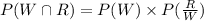
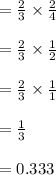
Likewise, the chip transmitted is presumably red
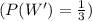 and the chip transferred is a red chip of urn II
and the chip transferred is a red chip of urn II
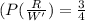 , and a red chip is likely to be red
, and a red chip is likely to be red
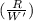 .
.
Finally,

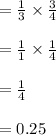
The estimation of
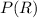 and
and
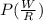 as:
as: