Question

Use the definition of continuity and the properties of limit to show that the function f(x)=x sqrtx/ (x-6)^2 is continuous at x=36.

Answer 1

The function
`\\ f(x) = (x*√(x))/((x-6)^(2))` is continuous at x = 36.

Explanation:

We need to follow the following steps:

The function is:

`\\ f(x) = (x*√(x))/((x-6)^(2))`

The function is continuous at point x=36 if:

1. The function
   `\\ f(x)` exists at x=36.
2. The limit on both sides of 36 exists.
3. The value of the function at x=36 is the same as the value of the limit of the function at x = 36.

Therefore:

The value of the function at x = 36 is:

`\\ f(36) = (36*√(36))/((36-6)^(2))`

`\\ f(36) = (36*6)/(900) = (6)/(25)`

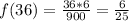
The limit of the
`\\ f(x)` is the same at both sides of x=36, that is, the evaluation of the limit for values coming below x = 36, or 33, 34, 35.5, 35.9, 35.99999 is the same that the limit for values coming above x = 36, or 38, 37, 36.5, 36.1, 36.01, 36.001, 36.0001, etc.

For this case:

`\\ lim_(x \to 36) f(x) = (x*√(x))/((x-6)^(2))`

`\\ \lim_(x \to 36) f(x) = (6)/(25)`

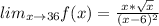
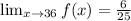
Since

`\\ f(36) = (6)/(25)`

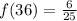
And

`\\ \lim_(x \to 36) f(x) = (6)/(25)`

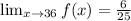
Then, the function
`\\ f(x) = (x*√(x))/((x-6)^(2))` is continuous at x = 36.