Question

Jeff bicycles 126 miles at the rate of r mph. The same trip would have taken 2 hours longer if he had decreased his speed by 4 mph. Find r. His original speed was r = _____________ mph.

Answer 1

Given Information:

Distance = 160 miles

Required Information:

Rate = r = ?

Answer:

Rate = r = 20 mph

Step-by-step explanation:

Recall that the rate is given by

Rate = distance/time

`r = (d)/(t) \\\\t = (d)/(r) \\\\t = (160)/(r) \\\\`

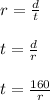
It is given that the same trip would have taken 2 hours longer if he had decreased his speed by 4 mph.

Mathematically,

`(160)/((r-4)) = (160)/(r) + 2 \\\\`

Simplify the equation

`(160)/((r-4)) - (160)/(r) = 2 \\\\(160r - 160(r-4))/(r(r-4)) = 2 \\\\(160r - 160r+640))/(r(r-4)) = 2 \\\\160r - 160r+640 = r(r-4) (2) \\\\640 = r(r-4) (2) \\\\640 = (r^2 - 4r) (2) \\\\640 = 2r^2 - 8r \\\\2r^2 - 8r-640 =0 \\\\2(r^2 - 4r-320) =0 \\\\r^2 - 4r-320 =0 \\\\`

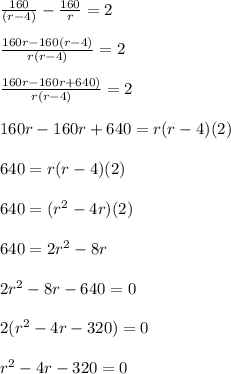
Now we are left with a quadratic equation.

We may solve the quadratic equation using the factorization method

`r^2 - 4r-320 =0 \\\\r^2-20r+16r-320=0 \\\\r(r-20)+16(r-20)=0 \\\\(r-20) (r+16)=0 \\\\`

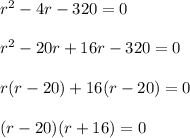
So,

`(r-20) = 0 \\\\r = 20 \\\\`

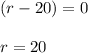
OR

`(r+16)=0 \\\\r = -16 \\\\`

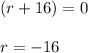
Since rate cannot be negative, discard the negative value of r

Therefore, the rate is

`r = 20 \: mph`