Question

You have been asked to design a rectangular box with a square base and an open top. The volume of the box must be 1536cm3. Determine the dimensions of the box that will minimize the surface area, where x is the length of each side of the base and y is the height of the box g

Answer 1

The dimensions of the box are:

Length = 11.53cm

Breadth = 11.53cm

Height = 11.53cm

Explanation:

The volume of the box can be calculated with this formula:

The volume of the box = area of square base X height of the box.

We are given that the length of one side of the square base is = x cm, and its height is h cm.

Area of square base =
`x^(2)cm^(2)`

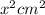
The surface area of the box will be minimized if the height of the box, is the same as its length. hence, we can take the height of the box to be x cm also.

In this case, the volume of the box will be
`x^(3)=1536cm^(3)`

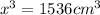
from this,
`x =3√(1536)= 11.53cm`

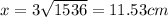
There fore, the box has its length, height, and width all having the same values.

The dimensions of the box are:

Length = 11.53cm

Breadth = 11.53cm

Height = 11.53cm