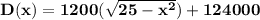Question

A firm has the​ marginal-demand function Upper D prime (x )equalsStartFraction negative 1200 x Over StartRoot 25 minus x squared EndRoot EndFraction . Find the demand function given that Dequals16 comma 000 when x equals $ 4 per unit.

Answer 1

The demand function is
`\mathbf{D(x) = 1200(√(25-x^2))+ 124000}`

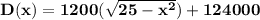
Explanation:

A firm has the​ marginal-demand function
`D' x = (-1200)/(√(25-x^2 ) )`.

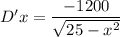Find the demand function given that D = 16,000 when x = $4 per unit.

What we are required to do is to find the demand function D(x);

If we integrate D'(x) with respect to x ; we have :

`\int\limits \ D'(x) \, dx = \int\limits{(-1200 x)/(√(25-x^2)) } \, dx`

`D(x) = \int\limits{(-1200 x)/(√(25-x^2)) } \, dx`

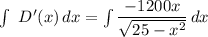
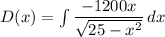
Let represent t with
`√(25-x^2)}`

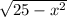
The differential of t with respect to x is :

`(dt)/(dx)= (1)/(2 √(25-x^2))}(-2x)`

`(dt)/(dx)= (-x)/( √(25-x^2))}`

`{dt}= (-xdx)/( √(25-x^2))}`

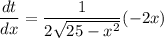
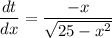
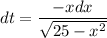
replacing the value of
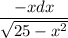`(-xdx)/( √(25-x^2))}` for dt in
`D(x) = \int\limits{(-1200 x)/(√(25-x^2)) } \, dx`

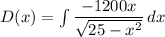
So; we can say :

`D(x) = \int\limits{(-1200 x)/(√(25-x^2)) } \, dx`

`D(x) = 1200\int\limits{(- x)/(√(25-x^2)) } \, dx`

`D(x) = 1200\int\limits \ dt`

`D(x) = 1200t+ C`

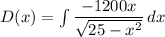
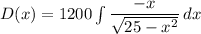
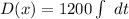
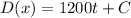
Let's Recall that :

t =
`√(25-x^2)}`

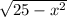
Now;

`\mathbf{D(x) = 1200(√(25-x^2)})+ C}`

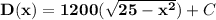
GIven that:

D = 16,000 when x = $4 per unit.

i.e

D(4) = 16000

SO;

`D(x) = 1200(√(25-x^2)})+ C`

`D(4) = 1200(√(25-4^2)})+ C`

`D(4) = 1200(√(25-16)})+ C`

`D(4) = 1200(√(9)})+ C`

`D(4) = 1200(3}})+ C`

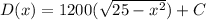
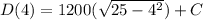
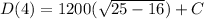
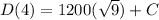
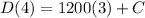
16000 = 1200 (3) + C

16000 = 3600 + C

16000 - 3600 = C

C = 12400

replacing the value of C = 12400 into
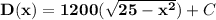`\mathbf{D(x) = 1200(√(25-x^2)})+ C}`, we have:

`\mathbf{D(x) = 1200(√(25-x^2))+ 124000}`

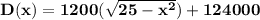
∴ The demand function is
`\mathbf{D(x) = 1200(√(25-x^2))+ 124000}`