Question

The length l, width w, and height h of a box change with time. At a certain instant the dimensions are l = 3 m and w = h = 6 m, and l and w are increasing at a rate of 3 m/s while h is decreasing at a rate of 6 m/s. At that instant find the rates at which the following quantities are changing.

(a) The volume.
m3/s
(b) The surface area.
m2/s
(c) The length of a diagonal. (Round your answer to two decimal places.)
m/s

Answer 1

a) The rate of change associated with the volume of the box is 54 cubic meters per second, b) The rate of change associated with the surface area of the box is 18 square meters per second, c) The rate of change of the length of the diagonal is -1 meters per second.

Explanation:

a) Given that box is a parallelepiped, the volume of the parallelepiped, measured in cubic meters, is represented by this formula:

`V = w \cdot h \cdot l`

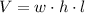
Where:

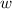`w` - Width, measured in meters.

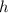`h` - Height, measured in meters.

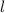`l` - Length, measured in meters.

The rate of change in the volume of the box, measured in cubic meters per second, is deducted by deriving the volume function in terms of time:

`\dot V = h\cdot l \cdot \dot w + w\cdot l \cdot \dot h + w\cdot h \cdot \dot l`

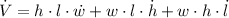
Where
`\dot w`,
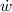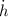`\dot h` and
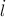`\dot l` are the rates of change related to the width, height and length, measured in meters per second.

Given that
`w = 6\,m`,
`h = 6\,m`,
`l = 3\,m`,
`\dot w =3\,(m)/(s)`,
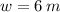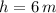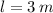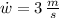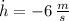`\dot h = -6\,(m)/(s)` and
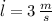`\dot l = 3\,(m)/(s)`, the rate of change in the volume of the box is:

`\dot V = (6\,m)\cdot (3\,m)\cdot \left(3\,(m)/(s) \right)+(6\,m)\cdot (3\,m)\cdot \left(-6\,(m)/(s) \right)+(6\,m)\cdot (6\,m)\cdot \left(3\,(m)/(s)\right)`

`\dot V = 54\,(m^(3))/(s)`

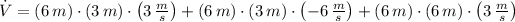
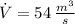
The rate of change associated with the volume of the box is 54 cubic meters per second.

b) The surface area of the parallelepiped, measured in square meters, is represented by this model:

`A_(s) = 2\cdot (w\cdot l + l\cdot h + w\cdot h)`

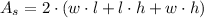
The rate of change in the surface area of the box, measured in square meters per second, is deducted by deriving the surface area function in terms of time:

`\dot A_(s) = 2\cdot (l+h)\cdot \dot w + 2\cdot (w+h)\cdot \dot l + 2\cdot (w+l)\cdot \dot h`

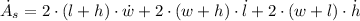
Given that
`w = 6\,m`,
`h = 6\,m`,
`l = 3\,m`,
`\dot w =3\,(m)/(s)`,
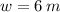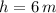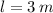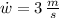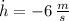`\dot h = -6\,(m)/(s)` and
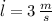`\dot l = 3\,(m)/(s)`, the rate of change in the surface area of the box is:

`\dot A_(s) = 2\cdot (6\,m + 3\,m)\cdot \left(3\,(m)/(s) \right) + 2\cdot (6\,m+6\,m)\cdot \left(3\,(m)/(s) \right) + 2\cdot (6\,m + 3\,m)\cdot \left(-6\,(m)/(s) \right)`

`\dot A_(s) = 18\,(m^(2))/(s)`

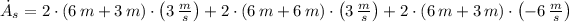
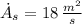
The rate of change associated with the surface area of the box is 18 square meters per second.

c) The length of the diagonal, measured in meters, is represented by the following Pythagorean identity:

`r^(2) = w^(2)+h^(2)+l^(2)`

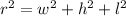
The rate of change in the surface area of the box, measured in square meters per second, is deducted by deriving the surface area function in terms of time before simplification:

`2\cdot r \cdot \dot r = 2\cdot w \cdot \dot w + 2\cdot h \cdot \dot h + 2\cdot l \cdot \dot l`

`r\cdot \dot r = w\cdot \dot w + h\cdot \dot h + l\cdot \dot l`

`\dot r = \frac{w\cdot \dot w + h \cdot \dot h + l \cdot \dot l}{\sqrt{w^(2)+h^(2)+l^(2)}}`

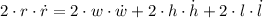
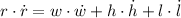
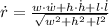
Given that
`w = 6\,m`,
`h = 6\,m`,
`l = 3\,m`,
`\dot w =3\,(m)/(s)`,
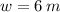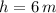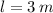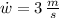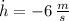`\dot h = -6\,(m)/(s)` and
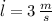`\dot l = 3\,(m)/(s)`, the rate of change in the length of the diagonal of the box is:

`\dot r = \frac{(6\,m)\cdot \left(3\,(m)/(s) \right)+(6\,m)\cdot \left(-6\,(m)/(s) \right)+(3\,m)\cdot \left(3\,(m)/(s) \right)}{\sqrt{(6\,m)^(2)+(6\,m)^(2)+(3\,m)^(2)}}`

`\dot r = -1\,(m)/(s)`

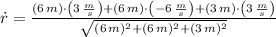
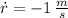
The rate of change of the length of the diagonal is -1 meters per second.