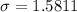Complete Question
The complete question is shown on the first uploaded image
Answer:
The standard deviation is
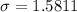
Explanation:
The sample size is n = 18
Generally the probability of getting a four in the toss of the fair die is mathematically represented as
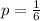
While the probability of not getting a four is
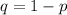
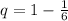
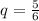
Now the standard deviation for the binomial random number is mathematically represented as

substituting values