Answer:
a) The work required to stretch the spring from 20 centimeters to 25 centimeters is 0.313 joules, b) The area of the region enclosed by one loop of the curve
 is
is
 .
.
Step-by-step explanation:
a) The work, measured in joules, is a physical variable represented by the following integral:

Where
 ,
,
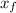 - Initial and final position, respectively, measured in meters.
- Initial and final position, respectively, measured in meters.
 - Force as a function of position, measured in newtons.
- Force as a function of position, measured in newtons.
Given that
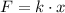 and the fact that
and the fact that
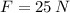 when
when
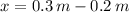 , the spring constant (
, the spring constant (
 ), measured in newtons per meter, is:
), measured in newtons per meter, is:
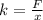
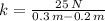
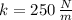
Now, the work function is obtained:
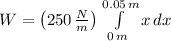
![W = (1)/(2)\cdot \left(250\,(N)/(m) \right)\cdot [(0.05\,m)^(2)-(0.00\,m)^(2)]](https://img.qammunity.org/2021/formulas/physics/college/28sxsyj74jwuhxrc7mwus7k3tyciwjwr0v.png)
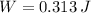
The work required to stretch the spring from 20 centimeters to 25 centimeters is 0.313 joules.
b) Let be
 . The area of the region enclosed by one loop of the curve is given by the following integral:
. The area of the region enclosed by one loop of the curve is given by the following integral:
![A = \int\limits^(2\pi)_0 {[r(\theta)]^(2)} \, d\theta](https://img.qammunity.org/2021/formulas/physics/college/x2wt4k1spwzaks3n89jc7uc7bhvatnhec7.png)
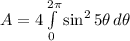
By using trigonometrical identities, the integral is further simplified:
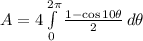

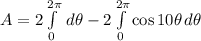
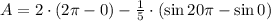
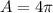
The area of the region enclosed by one loop of the curve
 is
is
 .
.