Question

If the variance of 3 4 6 y (y+3) and 9 is 21.6 what is the standard deviation of 6 8 12 2y (2y+6) and 18

Answer 1

The standard deviation of second data set is 9.2952.

Explanation:

The variance of a random variable is independent of change of origin but not of scale.

That is if any value is added or subtracted from the random variable then the variance of the random variable will not change.

`V(X+a)=V(X)+V(a)=V(X)`

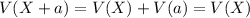
And if any value is multiplied or divided by the random variable then the variance of the random variable will change.

`V(aX)=a^(2)V(X)`

The first set of data is:

S₁ = {3, 4, 6, y, (y+3) and 9}

The variance of S₁ is,

V (S₁) = 21.6

The second set of data is:

S₂ = {6, 8, 12, 2y, (2y+6) and 18}

On comparing the two sets of data, it can be concluded that:

S₂ = 2 × S₁

Compute the variance of S₂ as follows:

`V(S_(2))=V(2* S_(1))`

`=2^(2)* V(S_(1))\\\\=4* 21.6\\\\=86.4`

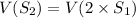
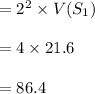
Then the standard deviation of S₂ is:

`SD(S_(2))=\sqrt{V(S_(2))}`

`=√(86.4)\\=9.2952`

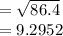
Thus, the standard deviation of second data set is 9.2952.