Question

If m ≤ f(x) ≤ M for a ≤ x ≤ b, where m is the absolute minimum and M is the absolute maximum of f on the interval [a, b], then m(b − a) ≤ b f(x) dx a ≤ M(b − a). Use this property to estimate the value of the integral. 1 0 x3 dx

Answer 1

m = 1.5

M = 3

Explanation:

According to the situation, the solution is as follows

Here we need to determine the maximum and minimum of

`f(x) = (3)/(1 + x^2)\ on\ 0,1`

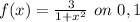
Now we have to differentiate it

`f(x)' = ((1 + x^2) * 0 - 3* 2x )/((1 + x^2)^2) \\\\ = (-6x)/((1 + x^2)^2)`

Now the points i.e x = 0 and x =1 could be tested

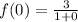
`f(0) = (3)/(1 + 0)`

= 3

`f(1) = (3)/(1 + 1)`

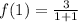
= 1.5

So,

m = 1.5

M = 3

By applying the differentiation we could easily estimate the value of the integral and the same is to be shown above