Answer:
9
Explanation:
Given that (1, 2) is the vertex of the function represented by the table of values above, the rate of change for the interval from x = 5 to x = 6.
f(5) = 18
f(6) = ?
=>Find f(6) using the vertex form function, f(x) = a(x - h)² + k
Where, h and k are the given vertex of the function = (1, 2).
h = 1, k = 2
Thus,
f(x) = a(x - 1)² + 2
Find the value of a by using any of the points given in the table.
Using (3, 6), we have the following,
6 = a(3 - 1)² + 2
6 = a(2)² + 2
6 = 4a + 2
Subtract 2 from both sides
6 - 2 = 4a
4 = 4a
Divide both sides by 4
1 = a
a = 1
Let's find f(6) using f(x) = a(x - 1)² + 2
Plug the value of a and x
f(6) = 1(6 - 1)² + 2
f(6) = 25 + 2
f(6) = 27
==>Find the rate of change/slope
f(5) = 18
f(6) = 27
Rate of change =
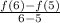
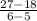
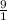
Rate of change = 9