Answer:
Option (3)
Explanation:
Volume of the flavored ice that can be filled in the cone = Volume of the ice cone - volume of the spherical piece of bubble gum
Volume of a cone =
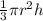
where r = radius of the cone
h = height of the cone
Volume of the ice cone =
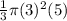
Volume of a sphere =
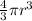 [r = radius of the bubble gum]
[r = radius of the bubble gum]
=
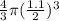
=
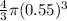
Volume of the flavored ice filled in the cone =

Therefore, Option (3) will be the answer.