Question

Find the surface area of each prism. Round to the nearest tenth if necessary while doing your calculations as well as in your final answer. 360 units2 586 units2 456 units2 552 units2

Answer 1

Option (4)

Explanation:

Surface area of a prism = 2B + P×h

where B = Area of the triangular base

P = perimeter of the triangular base

h = height of the prism

B =
`(1)/(2)(\text{leg 1})(\text{leg 2})`

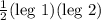
Since, (Hypotenuse)² + (Leg 1)² + (Leg 2)² [Pythagoras theorem]

(20)² = (12)² + (Leg 2)²

Leg 2 =
`√(400-144)`

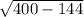
= 16 units

Therefore, B =
`(1)/(2)* 12* 16`

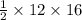
= 96 units²

P = 12 + 16 + 20

P = 48 units

h = 7.5 units

Surface area of the prism = 2(96) + (48×7.5)

= 192 + 360

= 552 units²

Therefore, surface area of the given triangular prism = 552 units²

Option (4) will be the answer.