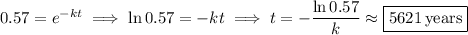The half-life
 is the amount of time it takes for some quantity
is the amount of time it takes for some quantity
 of carbon-14 to decay to half the original amount, or
of carbon-14 to decay to half the original amount, or
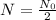 .
.
In terms of the formula, it's the time such that
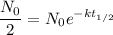
and we can divide both sides by the original amount to get
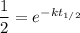
We want to find the time
 it takes for 57%, or 0.57, of the original amount to remain. This means we solve for
it takes for 57%, or 0.57, of the original amount to remain. This means we solve for
 in
in

or
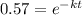
We're given
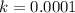 ; plug this in and solve for
; plug this in and solve for
 :
: